Next: 4 Applications Up: 3 Well-known distributions Previous: 3.1 Binomial distribution
The probability distribution function requires two pieces of information.
![]() is usually used to denote ``how many events'', and
is usually used to denote ``how many events'', and ![]() is usually
used to indicate the expected number of occurances. Thus, in our
example,
is usually
used to indicate the expected number of occurances. Thus, in our
example, ![]() because we are interested in the probability that only
three busses arrive. However,
because we are interested in the probability that only
three busses arrive. However,
![]() because on the average,
a bus arrives every 15 minutes, so there should have been 8 busses
over 120 minutes.
because on the average,
a bus arrives every 15 minutes, so there should have been 8 busses
over 120 minutes.
In order to apply Poisson probability distribution, we need to
assume that the probability of
the first event happening after a period of ![]() is
is
![]() , where
, where
![]() is the expected number of occurances in time
is the expected number of occurances in time ![]() .
.
The random variable (function) ![]() is usually defined as the number of
occurances.
is usually defined as the number of
occurances.
The probability function is as follows:
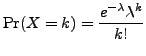 |
(3) |
In many cases, we are more interested in the cumulative probability. In other words, we want to know ``what are the chances that on the average, a bus is late in two hours''?
This probability can be expressed as follows:
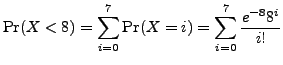
Copyright © 2006-10-09 by Tak Auyeung