3.1 Binomial distribution

Assume that we have a coin that is loaded. We know that the probability of getting heads up is $p$ , which automatically means that the probability of getting tails up is $1-p$ . If I flip the coin 5 times, what is the probability that I end up with 2 heads up?

Since we don't care about the actual ordering of heads and tails, we need to consider the following permutations:

• HHTTT
• HTHTT
• HTTHT
• HTTTH
• THHTT
• THTHT
• THTTH
• TTHHT
• TTHTH
• TTTHH

The probability of each permutation is $p^2(1-p)^3$ . Consequently, the overall probability of getting 2 heads and 3 tails from 5 flips is $10\cdot p^2(1-p)^3$ .

When we generalize binomial distribution, it is conventional to use the term ``successful'' and ``fail'' to describe the result of each experiment. Therefore, our question becomes as follows.

In general, given the probability of success is $p$ , $n$ trials, and $r$ successful results, what is the overall probability of such a combination?

We need to first figure out the number of permutations of $r$ successes and $n-r$ failures from $n$ trials. This number turns out to be $n \choose r$ ($n$ choose $r$ )!

To explain this, let us assume $s_i$ represents success in experiment $i$ . Then, we can construct a set $T = \{s_1, s_2, \ldots s_n\}$ to represent all the successful experiments (within $n$ trials).

When we say that we want to have $r$ successes, that means we need to select $r$ elements from the set $T$ . This brings us back to module 0058. There are $n \choose r$ subsets of $r$ elements from set $T$ (which has $n$ elements).

We can quickly apply this to our coin-flipping example. We are to flip a coin five times, and want to find out the number of permutations that have to heads. By enumeration, we ended with 10 permutations. However, by calculation, ${5 \choose 2} = \frac{5!}{2!3!} = \frac{120}{2\cdot 6} = 10$ !

The random variable (function) of binomial distribution is often chosen to be the number of successes (in $n$ experiments). As a result, the range of the random variable (function) is $\{0,1,2,3,\ldots n\}$ . This means that:

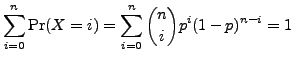$$\sum_{i=0}^{n}{\rm Pr}(X=i) = \sum_{i=0}^{n} {n \choose i}p^i(1-p)^{n-i} = 1$$ (1)

The binomial distribution has many applications. For example, let us assume that the probability of a student passing a class with a letter grade of `B' or better is 0.3. Assume we have a class of 20 students. We can now answer the question of ``what are the chances that at least 10 students pass the class with a letter grade of `B' or better?''

The answer is as follows:

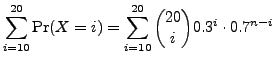$$\sum_{i=10}^{20} {\rm Pr}(X=i) = \sum_{i=10}^{20} {20 \choose i}0.3^i\cdot 0.7^{n-i}$$ (2)