4 Applications

Both binomial and Poisson distributions are very useful in the context of computer science and electrical engineering. As discussed, the binomial distribution is useful to model the likelihood of outcomes from Bernoulli processes. On the other hand, the Poisson distribution is useful to model the likelihood of asynchronous events.

For example, we can experiment and find out the per-bit error rate in a noisy environment. Let us even assume the probability of misinterpreting a one as a zero is the same as that of a zero as a one. (This is generally not true.) This error rate $e$ is the failure probability. As a result, $p=1-e$ . If we send a packet of 256 bits, what are the chances that there is at least one bit of error?

We can use binomial distribution to solve this problem:

$${\rm Pr}(X \ge 1) = \sum_{i=1}^{256} {\rm Pr}(X = i) = \sum_{i=1}^{256} {256 \choose i}e^i(1-e)^(256-i)$$

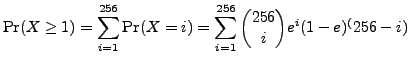
Let us consider another example. Assume that during peak hours, a particular web site has an average of 50 hits per minute. Let us assume that hits of a web site follows the Poisson distribution. We need to ensure there is enough processing power to handle the peak hours. If we test the server to be able to handle 100 hits per minute, what are the chances that it will be overwhelmed (and start to have requests queued up)?

Let us use the average number of hits per minute as $\lambda$ . In other words, $\lambda = 50$ . Then the probability of having more than 100 hits per minute is as follows:

$${\rm Pr}(X > 100) = \sum_{i=101}^{\infty} {\rm Pr}(X = i) = \sum_{i=101}^{\infty} \frac{e^{-50}50^{i}}{i!}$$

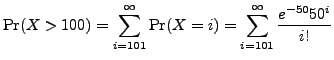
If you have a calculator handy, you will find that this number is very small.