Next: 6 The pigeon hole Up: Module 0058: Counting is Previous: 4.2 Combinations
For row ![]() , there are exactly
, there are exactly ![]() columns. The first and last columns
of each row,
columns. The first and last columns
of each row, ![]() and
and ![]() , must be 1. All other columns are
defined as follows
, must be 1. All other columns are
defined as follows
![]() .
.
This yields a ``triangle'' as represented in table 1.
Because of the symmetry of the triangle, you only need to figure out one half (left or right), and the other half is the same.
Here is the interesting part.
![]() . For example,
. For example,
![]() , this means that
, this means that
![]() . Of course, we can
easily verify that
. Of course, we can
easily verify that
![]() .
.
How does this work, in general? At the core, we need to prove that
![]() .
.
The proof is as follows:
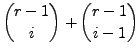 |
(9) | ||
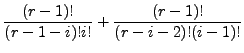 |
(10) | ||
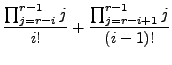 |
(11) | ||
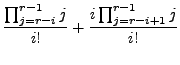 |
(12) | ||
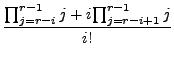 |
(13) | ||
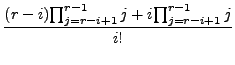 |
(14) | ||
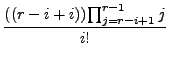 |
(15) | ||
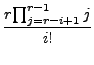 |
(16) | ||
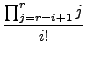 |
(17) | ||
| (18) | |||
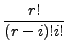 |
(19) | ||
| (20) |
Copyright © 2006-10-11 by Tak Auyeung