Next: 6 External resources Up: Module 0035: Proof by Previous: 4 Example 1
The base case is simple (when ![]() ):
):
![]() .
.
The induction step states that
![]() . We need to
assert this proposition:
. We need to
assert this proposition:
| (5) | |||
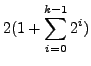 |
(6) | ||
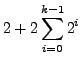 |
(7) | ||
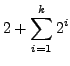 |
(8) | ||
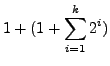 |
(9) | ||
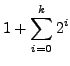 |
(10) |
Because we proved the base case and also the induction step, we conclude that the original proposition is true.
Copyright © 2006-09-11 by Tak Auyeung