Next: 5 Example 2 Up: Module 0035: Proof by Previous: 3 Ordinary (not so
The predicate, ![]() , states that
, states that
![]() .
.
The base case is ![]() .
.
![]() , but
, but
![]() .
Therefore, the base case is proven.
.
Therefore, the base case is proven.
Note that our ![]() in this case. In other words, we only have one
base case.
in this case. In other words, we only have one
base case.
Next, we need to show that
![]() .
In other words, for all
.
In other words, for all ![]() , if we know that
, if we know that
![]() , how can we show that
, how can we show that ![]() ?
?
Well, ![]() means that
means that
![]() . Then,
we can add
. Then,
we can add ![]() to both sides so that we have
to both sides so that we have
![]() .
The right hand side can be transformed as follows:
.
The right hand side can be transformed as follows:
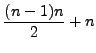 |
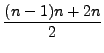 |
(1) | |
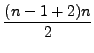 |
(2) | ||
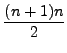 |
(3) | ||
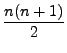 |
(4) |
As a result, ![]() is true.
is true.
Note that we only had to make use of the fact that ![]() in order to
prove that
in order to
prove that ![]() . In other words, we only made use of ordinary induction,
but not strong induction.
. In other words, we only made use of ordinary induction,
but not strong induction.
Copyright © 2006-09-11 by Tak Auyeung