A discrete probability distribution function is a probability function
that has a discrete domain. This means the domain either has a finite
number of elements, or it is countably infinite. The set of all integers
(
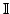 ) is infinite, but it is countably infinite. On the other
hand, the set of all real numbers, (
) is infinite, but it is countably infinite. On the other
hand, the set of all real numbers, (
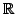 ), is not countably
infinite.
), is not countably
infinite.
Subsections
Copyright © 2006-10-09 by Tak Auyeung