4.1 Permutation

As discussed earlier, ordering is important in a permutation. In general, the set of all permutations (given $n$ elements, and picking $r$ from the set) is as follows:

$P(X, r) = \{(e_1,\ldots e_r)\vert e_1 \in X, e_2 \in X \setminus \{e_1\}, e_3 \in X \setminus \{e_1, e_2\}, \ldots e_r \in X \setminus \{e_1, \ldots e_{r-1}\}\}$ .

There are $n$ elements to select from for the first element, $e_1$ in each tuple. There are $n-1$ elements to choose from for the second element, and etc. By the time we get to the $r^{\rm th}$ item, there are $n-r+1$ items to choose from.

Because the selection of elements is a sequence, and each step is independent from the next one, we need to use the product rule. This means that

$\vert P(X,r)\vert = \vert X\vert\cdot (\vert X\vert-1) \cdots (\vert X\vert-r+1)$

Since we make $n=\vert X\vert$ , we can shorten the formula to

$_n P_r = \vert P(X,r)\vert = \prod_{i=1}^{r} (n-i+1)$

Note that $_nP_r$ is just another way to count the number of possible permutations of selecting $r$ from $n$ items.

Although we can use the $\prod$ symbol, it is still a handful to have to spell out the product term. To make it easier, we define factorial as follows:

$(n > 0) \Rightarrow n! = \prod_{i=1}^{n} i$

and

$(n = 0) \Rightarrow n! = 1$

With this definition, we can rewrite the number of permutations as follows (when $r < n$ ):

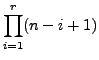$$_n P_r = \prod_{i=1}^{r} (n-i+1)$$ (1)

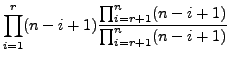$$= \prod_{i=1}^{r} (n-i+1) \frac{\prod_{i=r+1}^{n} (n-i+1)}{\prod_{i=r+1}^{n} (n-i+1)}$$ (2)

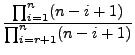$$= \frac{\prod_{i=1}^{n} (n-i+1)}{\prod_{i=r+1}^{n} (n-i+1)}$$ (3)

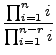$$= \frac{\prod_{i=1}^{n} i}{\prod_{i=1}^{n-r} i}$$ (4)

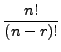$$= \frac{n!}{(n-r)!}$$ (5)

Interestingly, this formula works even when $n = r$ because we define $0! = 1$ .