Many relations have the same set for domain and range. These relations
may have additional attributes.
- Reflexive:
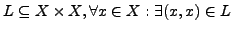
- Symmetric:
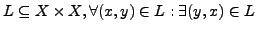
- Antisymmetric:
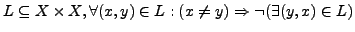
- Transitive:
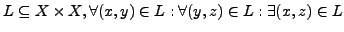
- Total:
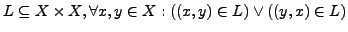 . Total implies reflexive.
. Total implies reflexive.
Let us consider some examples:
- Real number equality. It is reflexive because
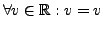 . It is symmetric because
. It is symmetric because
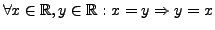 .
It is also transitive because
.
It is also transitive because
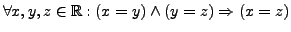 . It is not total because
. It is not total because 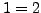 and
and 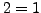 are both
false. It is antisymmetric.
are both
false. It is antisymmetric.
- Real number
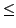 (less-than-or-equal-to).
It is reflexive because
(less-than-or-equal-to).
It is reflexive because
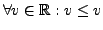 . It is not symmetric because
. It is not symmetric because 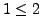 , but
, but
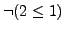 .
It is transitive because
.
It is transitive because
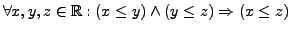 . It is total and antisymmetric.
. It is total and antisymmetric.
- Real number
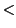 (less-than). It is not reflexive because
(less-than). It is not reflexive because
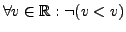 . It is not symmetric
because
. It is not symmetric
because
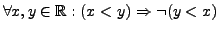 .
Last, but not least, it is transitive because
.
Last, but not least, it is transitive because
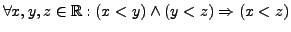 . It is not total, but it is antisymmetric.
. It is not total, but it is antisymmetric.
- Positive integers ``is a factor of''.
It is reflexive because each integer is its own factor.
It is not symmetric because 3 is a factor of 9, but 9 is not a
factor of 3. It is transitive because if
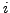 is a factor of
is a factor of 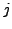 ,
and
,
and 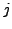 is a factor of
is a factor of 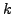 , then
, then 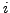 is a factor of
is a factor of 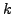 . This
relation is not total, and it is antisymmetric.
. This
relation is not total, and it is antisymmetric.
There are special names for relations that satisfy a combination of
properties:
- Partial order: reflexive, antisymmetric and transitive
- Total order: total, antisymmetric and transitive
- Equivalence: reflexive, symmetric and transitive
Copyright © 2006-09-26 by Tak Auyeung