5 Center of mass and ``weight shifting''

The center of mass of a vehicle is the one point at which you can imagine the entire mass of the vehicle is. When a vehicle is stationary, the center of mass is also the center of gravity. However, when a vehicle is accelerating, decelerating or cornering, the center of gravity ``shifts''.

The gravitational force of a vehicle points directly to the center of the earth. An additional force, such as acceleration or braking, can change the total vector of force acting on the vehicle.

For example, in our example, a Miata can achieve an acceleration of $6.75ms^{-2}$ horizontally. When this is combined with the gravity of $9.8ms^{-2}$ vertically, the total force acting on a Miata is $({6.75}^{2}+{9.8}^{2})^{-2}=11.90$, pointing at a direction that is about 55.44 degrees down to the rear.

This is pictorially represented here:

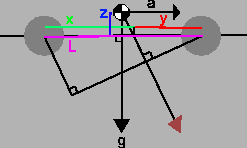
``L'' is the length between the two axles. ``g'' is gravity, and ``a'' is acceleration. ``z'' is the distance between the axle height and the center of mass. $x=\frac{L}{2}+z\frac{a}{g}$, $y=\frac{L}{2}-z\frac{a}{g}$.

Assuming the total weight of the vehicle is ``w'', the weight on the front (left) axle is $w_f=w\frac{y}{L}$, and the weight on the rear (right) axle is $w_r=w\frac{x}{L}$.

Note the proportion of weight shift depends not only on ``a'' (acceleration), but also ``z''. A lower profile vehicle, therefore, experiences less weight shift.